In the previous sections we have established the following two important results:
The first of these results implies that in order to obtain an optimal
solution of an LP, we can constrain our search on the set of the
extreme points of its feasible region. The second result provides an
algebraic characterization of this set: each of these points is
determined by selecting a set of basic variables, with
cardinality equal to the number of the technological constraints of
the LP, and the additional requirement that the (uniquely determined)
values of these variables are nonnegative (cf. discussion on
basic feasible solutions). This further implies that the set of
extreme points for an LP with m technological constraints and N
variables in its ``standard form'' representation can have only a
finite number of extreme points; specifically, 
is
an upper bound for the cardinality of this set.
The last observation would make one think that a (naive) approach to
the problem would be to enumerate the entire set of extreme points,
compare their corresponding objective values, and eventually select
one which minimizes the objective function over this set. Such an
approach would actually work for rather small formulations. But for
reasonably sized LP's, the set of extreme points, even though finite,
can become extremely large. For example, a small LP with 10 variables
(in ``standard form'') and 3 technological constraints can have upto
120 extreme points, while an LP with 100 variables and 20 constraints
can have upto 
extreme points. And yet, this is a
rather small LP!
Hence, we need a more systematic approach to organize the search so that we manage the complexity resulting from the size of the search space. Such a systematic approach is provided by the Simplex algorithm. The basic logic of the algorithm is depicted in Figure 12.
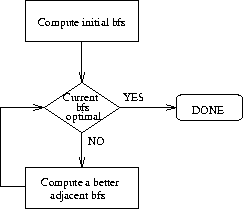
Figure 12: The basic Simplex logic
The algorithm starts with an initial basic feasible solution (bfs) and tests its optimality. If some optimality condition is verified, then the algorithm terminates. Otherwise, the algorithm identifies an adjacent bfs, with a better objective value. The optimality of this new solution is tested again, and the entire scheme is repeated, until an optimal bfs is found. Since every time a new bfs is identified the objective value is improved (except from a certain pathological case that we shall see later), and the set of bfs's is finite, it follows that the algorithm will terminate in a finite number of steps (iterations).
It is also interesting to examine the geometrical interpretation of the behavior of Simplex algorithm. Given the above description of the algorithm and the correspondence of bfs's to extreme points, it follows that Simplex essentially starts from some initial extreme point, and follows a path along the edges of the feasible region towards an optimal extreme point, such that all the intermediate extreme points visited are improving (more accurately, not worsening) the objective function.
In the following, we explain how the Simplex algorithm implements this logic in its computations by appplying it on our prototype LP.