Modern last-mile logistics systems are more and more frequently configured to provide rapid order fulfillment directly to consumers. The fastest are the same-day delivery systems, which promise that e-commerce orders received by a deadline during a day are delivered by the end of the same day (or, in some cases, within a few hours).
Same-day delivery fulfillment systems intend to provide consumers with the highest level of service in e-commerce. When a consumer places a same-day delivery order, they receive the product within an order lead time similar to that achieved when making a retail store trip in the afternoon or evening after the workday. Like any e-commerce order, product availability is known immediately at the order placement time. Additionally, a trip to the store is not required and it is likely that a larger product catalog is available.
Implementing same-day delivery systems in practice depends on building an effective vehicle dispatching plan. Such a plan should specify whether to operate a dedicated (owned) delivery fleet or whether to rely, at least in part, on outsourced delivery trips. Given this fleet strategy, the key question is how to assign delivery orders to vehicle dispatches. Once assigned, orders can be sequenced within a dispatch using standard ideas.
Here at Georgia Tech, Mathias Klapp worked with Alejandro Toriello and me on starting to build an understanding of vehicle dispatching forsame-day delivery systems in his Ph.D. thesis, completed near the end of 2016. Mathias is now on the transportation and logistics faculty at the Pontificia Universidad Católica de Chile, and the papers from his thesis are now coming out.
The first paper considers a simple setting, where a dedicated single vehicle is available to serve same-day delivery orders Klapp, M., Erera, A. L., & Toriello, A. (2018). The One-Dimensional Dynamic Dispatch Waves Problem. Transportation Science, 52, 402–415. https://doi.org/10.1287/trsc.2016.0682. This model is appropriate when a delivery region surrounding a distribution point is partitioned among multiple vehicles a priori, and we can therefore consider the operations of each vehicle separately. We study a key problem in same-day dispatching, specifically when to dispatch the vehicle during the operating day and with which delivery orders. In typical vehicle routing settings, orders are consolidated over some time period and then loaded into a vehicle for a single dispatch. Doing so can be quite cost effective, spreading the fixed vehicle dispatch cost over many orders and also reducing the variable travel costs (typically proportional to miles traveled) per order delivered.
This effectiveness is achieved via consolidation of a full day’s worth (in terms of required delivery time) of orders, which in turn requires that these orders are placed, picked, and packed prior to the operating day. We can try to mimic this approach in the same-day delivery setting, but it would require that the order deadline must occur substantially earlier in time than the delivery deadline. For example, to deliver by 8 pm with a 10-hour vehicle shift would mean an order deadline no later than 10 am!
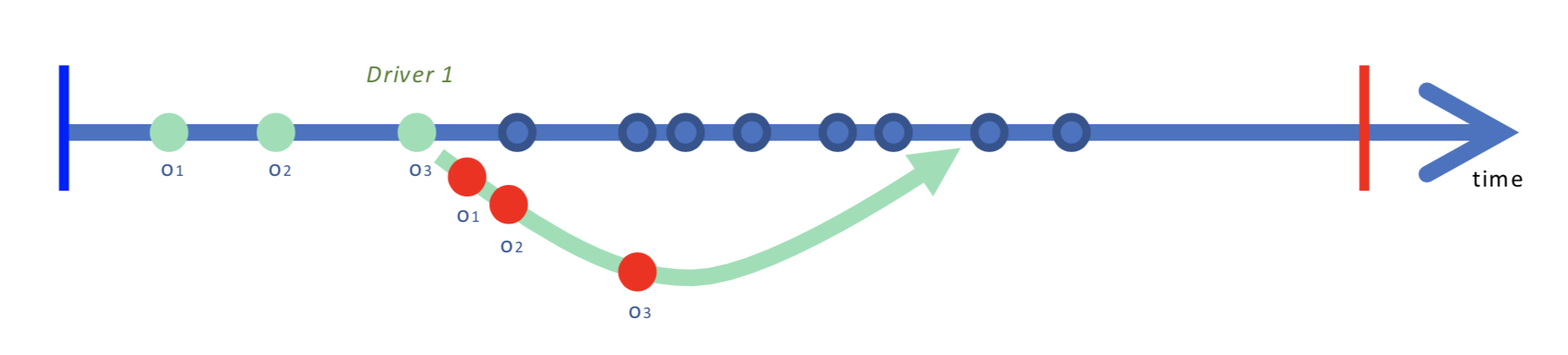
Therefore, we need to develop a better understanding of vehicle routing systems where some orders become ready while vehicles are making other deliveries. Each vehicle may need to be dispatched from the distribution point multiple times during the operating day. The figure above demonstrates the idea with a simple timeline. When should we stop waiting and dispatch the vehicle for the first time? Waiting allows orders to accumulate reducing the delivery cost per order, but simultaneously reduces available vehicle operating time before the ultimate delivery deadline. Should the vehicle wait after it returns to the distribution point? The figure also makes an assumption that need not be optimal in practice: that all available orders are loaded onto the vehicle each time it is dispatched. Sometimes it would be wiser to leave behind some orders that are not geographically compatible with the others, and hope that they can be grouped with better matches in a later dispatch.
In Klapp, M., Erera, A. L., & Toriello, A. (2018). The One-Dimensional Dynamic Dispatch Waves Problem. Transportation Science, 52, 402–415. https://doi.org/10.1287/trsc.2016.0682, we simplify the problem in one more way: we suppose that all geography in the problem can be modeled by mapping order delivery locations onto positions along a half-line extending from the distribution point. This approximation allows us to remove the sequencing complexity found in most routing problems (like the TSP), and focus more squarely on the multiple dispatch questions above. Why? Because the routing distance required to serve a group of orders is simply twice the distance to the furthest order to be delivered.
For this setting, we formulate a dynamic programming optimization model to determine when to dispatch a vehicle and with which orders, to minimize the cost of serving orders plus penalties for not providing same-day delivery service to some orders by the delivery deadline. Solving this DP even with the simplified geometry is very difficult in general when orders are described by a stochastic process. On the other hand, we show that deterministic variants of the problem where the order release times are known a priori can be solved with a polynomial dynamic program. We then show that a simple expectation minimization problem that we denote the a priori optimization problem can be solved with the same approach when order arrival times are modeled with a discrete distribution. The a priori problem is to select dispatch times and distances for the vehicle in advance for the remaining operating period that minimize expected costs, assuming that these dispatch times and distances cannot be adjusted. Finally, we use this a priori model and solution approach in a rollout approximation algorithm for the full dynamic problem in which a new potential dispatch plan is made for the vehicle at every time epoch when the vehicle dwells at the distribution point.
Please see the paper if you are interested in seeing more of the details. In the next blog post, I’ll discuss more about the results we found for this problem and extensions to problems with more realistic geography in the follow-up paper, also published in the same year Klapp, M., Erera, A. L., & Toriello, A. (2018). The Dynamic Dispatch Waves Problem for Same-day Delivery. European Journal on Operational Research, 271, 519–534. https://doi.org/10.1016/j.ejor.2018.05.032.
Here are the papers cited in this post if you’d like to learn more:
- Klapp, M., Erera, A. L., & Toriello, A. (2018). The One-Dimensional Dynamic Dispatch Waves Problem. Transportation Science, 52, 402–415. https://doi.org/10.1287/trsc.2016.0682
- Klapp, M., Erera, A. L., & Toriello, A. (2018). The Dynamic Dispatch Waves Problem for Same-day Delivery. European Journal on Operational Research, 271, 519–534. https://doi.org/10.1016/j.ejor.2018.05.032