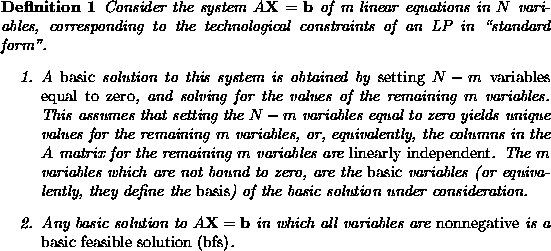For LP's in ``standard form'' the previous characterization of extreme points as the solution of n linearly independent binding constraints, which is, furthermore, a feasible point, can become even more concise. Consider, for instance, the LP
with m technological constraints and n variables. In ``standard form'', it becomes:
where I is the 
identity matrix, and 
is the vector of slack variables. It is
interesting to notice that for every binding constraint from the m+n
constraints of the original formulation (Eq. 25), one of
the m+n variables of the ``standard form'' formulation must be equal
to 0. Specifically, if the i-th technological constraint is binding,
the corresponding slack variable 
. Similarly, if one of the
sign restriction constraints is binding, then the corresponding
varialbe 
. Since an extreme point of the feasible region of
formulation 25 requires n binding constraints for its
definition, it follows that n from the n+m variables in the
corresponding solution of the ``standard form'' formulation
(Eq. 26) must be equal to zero. Furthermore, since this
point is uniquely defined, the system of equations defined by the m
technological constraints in the ``standard form'' formulation and the
m remaining variables, must have a unique solution. In other words,
the columns of the ``standard form'' formulation corresponding to
these m variables must be linearly independent (and their
determinant must have a nonzero value). Finally, since the extreme
point considered belongs in the feasible region of the problem, it
follows that the unique solution of the aforementioned system of m
equations in the m nonzero variables must be nonnegative (to meet
the sign restrictions required by ``standard form'').
The structure of the ``standard form'' solutions corresponding to
extreme points of the original feasible region (i.e., that defined
with respect to the primary LP variables 
), described for the
example above, actually applies to any other LP in ``standard
form''. We formally characterize this structure through the definition
of basic feasible solutions for LP's in ``standard form'' (taken
from Winston, ``Introduction to Mathematical Programming'').
