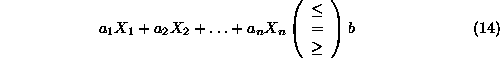
n-var LP's require an n-dimensional space to ``geometrically'' represent a vector corresponding to a pricing of their decision variables. However, the concepts and techniques that allowed the geometric representation of the 2-var LP's in the previous section, generalize quite straightforwardly in this more complicated case.
Hence, given a linear constraint:
and a point 
satisfying Equation 14 as equality, we can perceive the
solution space of
as the set
of points 
for which the vector 
is at right angles with vector 
,
as the set
of points for which the vector forms an acute angle with vector , and
as the set
of points for which the vector forms an obtuse angle with vector .
From the above description, it follows that the solution space of the
equation 
, i.e., the 3-dim case, is a
plane perpendicular to vector 
, which is
characterized as the plane normal. Since this normality
concept carries over to the more general n-dim case, we characterize
the solution space of an n-var linear equation as a
hyperplane. Furthermore, similar to the 2-var LP case, a hyperplane
defined by the equation ,
divides the n-dim space into two half-spaces: one of them is
the solution space of the inequality 
, and the other one is the solution space of the inequality
.
Hence, the solution space (feasible region) of an n-var LP is geometrically defined by the intersection of a number of half-spaces and/or hyperplanes equal to the LP constraints, including the sign restrictions. Such a set is characterized as a polytope. In particular, a bounded polytope is called a polyhedron.
Two other concepts of interest in the following discussion are those
of the straight line and the line segment. Given two
points 
and 
, the straight line
passing through them is algebraicaly defined by the set of
points
Figure 7 provides a visualization of this definition.
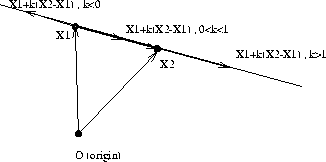
Figure 7: The equation of a straight line
As it is seen in the figure above, the line segment between
points 
and 
is analytically defined by:
Notice that Equation 16 can be rewritten as:
or
We say that Equations 17 and 18
define a convex combination of points and .
