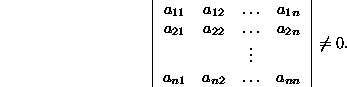Next: Example:
Up: No Title
Previous: The Fundamental Theorem of
In the previous section we showed that if an LP has a (bounded)
optimal solution, then it has (at least) one which corresponds to an
extreme point of its feasible region. To exploit this result
algorithmically, we need an algebraic characterization of the
extreme point concept. This is the topic of this section.
The starting point of this discussion is the observation made at the
end of the previous section, that at an extreme point, the set of
binding constraints is such that it characterizes the point
uniquely. Let's try to investigate what is the algebraic structure
implied by this statement. Also, staying close to the general spirit
of our discussion, let's examine this issue in an inductive
manner.
- We know that in the 1-dim space, i.e., on the line of real
numbers, a point can be identified uniquely by an equation a X = b,
where
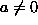 .
. - In the 2-dim space, a linear equation
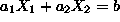 defines a line, i.e., a subspace with 1 ``degree of freedom'', while
the definition of a unique point requires a system of two linear
equations:
defines a line, i.e., a subspace with 1 ``degree of freedom'', while
the definition of a unique point requires a system of two linear
equations:


with a unique solution, i.e., with

Such a system of equations is characterized as
linearly independent, and geometrically, it corresponds to two
intersecting straight lines.
- In the 3-dim space, a linear equation
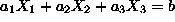 corresponds to a plane perpendicular to the vector
corresponds to a plane perpendicular to the vector
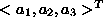 .
A system of two linear equations:
.
A system of two linear equations:
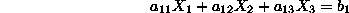
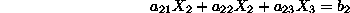
for which:
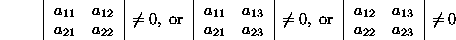
corresponds to the intersection of two planes, i.e., a
straight line.
Defining a unique point in the 3-dim space requires three
linearly independent equations, i.e.,
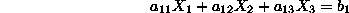
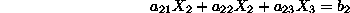
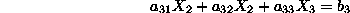
with
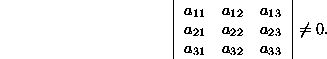
- In a similar fashion, in the n-dim space, a point is uniquely
defined by n linear equations which are linearly
independent, i.e.,
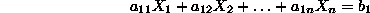
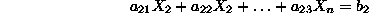

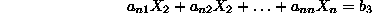
with
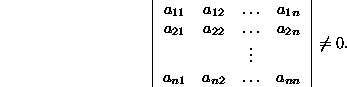



Next: Example:
Up: No Title
Previous: The Fundamental Theorem of
UAL Data
Fri Jun 20 15:03:05 CDT 1997
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
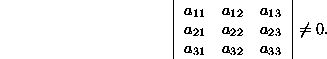
![]()
![]()
![]()
![]()