The SSLP Test Problems

Contributed by Lewis Ntaimo and Suvrajeet Sen

The test problem suite consists of data and computational results for 12 two-stage stochastic mixed-integer programs arising in stochastic server location problems (SSLPs). The problem formulation and instance generation are described in [1, 2]. The problems have pure binary first-stage variables, mixed-binary second-stage variables, and discrete distributions.

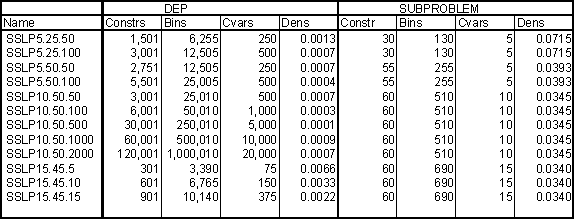
The following table presents the sizes of the deterministic equivalent and subproblem for each of the 12 problems instances. The instances are named SSLPm.n.s, where m is the number of potential server locations, n is the number of potential clients, and s is the number of scenarios.  Constrs, Bins, Cvars and Dens refer to the number of constraints, binary variables, continuous variables, and density of the constraint matrix, respectively.  The data for the each problem is given as three text files in SMPS format (TIME, CORE, and STOCH files). The SMPS data files are contained in the zip file sslp.zip .

Table 1:  Dimensions for the SSLP Instances

Computational results using an implementation of the D² algorithm [3] on a Sun 280R with UltraSPARC-III+ CPU running at 900 MHz are given in Table 2. The CPLEX 7.0 Callable Library [4] was used for solving the master and subproblems. To solve the large-scale SSLP DEP formulation for each of the problem instances the CPLEX MIP solver parameters were set at the following values: ``set mip emphasis 1" (emphasizes looking for feasible solutions), ``set mip strategy start 4" (uses barrier at the root), and        ``branching priority order on x (first-stage decision variables -- first branches on any fractional component of x before branching on y – second-stage decision variables). A CPU time limit of 10,800 seconds (3 hrs) was imposed and any problem instance run taking more than this time limit was stopped and the percent gap from optimality reported. All the problems that took less than this time limit converged to an optimal solution and the percentage gap between the lower bound and the upper bound was equal to 0%.         

Table 2: Computational Results for SSLP using the D² Algorithm

[1] Ntaimo, L. and S. Sen, “The ‘million-variable’ march for stochastic combinatorial optimization,” Journal of Global Optimization, to appear, 2004.

[2] Ntaimo, L. Decomposition algorithms for stochastic combinatorial optimization: Computational experiments and extensions, Ph.D. Dissertation, University of Arizona, 2004.

[3] Sen, S. and J.L. Higle, “The C³ Theorem and a D² Algorithm for Large Scale Stochastic Mixed-Integer Programming: Set Convexification,” Mathematical Programming, to appear, 2004.

[4] ILOG CPLEX, CPLEX 7.0 Users Manual and Reference Manual, ILOG CPLEX Division, Incline Village, NV, 2000.