
The Vehicle Routing Problem with Backhauls (VRPB) is an extension
of the classical Vehicle Routing Problem (VRP) that includes both
a set of customers to whom products are to be delivered, and a
set of vendors whose goods need to be transported back to the
distribution center. In addition, on each route all deliveries
have to be made before any goods can be picked up to avoid rearranging
the loads on the vehicle. The primary objective of this paper
is to present a new heuristic, called LHBH, for the VRPB. The
LHBH heuristic is based on the Generalized Assignment Problem
(GAP), and introduces new effective methods for generating an
initial solution and for locating the individual routes. Results
of a computational study, comparing the LHBH algorithm with other
heuristics and a lower bound, show the LHBH heuristic to be a
practical and effective solution approach for realistically sized
VRPB problems.
The Vehicle Routing Problem with Backhauls (VRPB), also known as the linehaul-backhaul problem, is an extension of the VRP involving both delivery and pickup points. Linehaul (delivery) points are sites that are to receive a quantity of goods from the single DC. Backhaul (pickup) points are sites that send a quantity of goods back to the DC. The critical assumption is that all deliveries must be made on each route before any pickups can be made. This arises from the fact that the vehicles are rear-loaded, and rearrangement of the loads on the trucks at the delivery points is not deemed economical or feasible. The quantities to be delivered and picked up are fixed and known in advance. The vehicle fleet is assumed to be homogeneous, each having a capacity of some weight or volume. Hence, a feasible solution to the problem consists of a set of routes where all deliveries for each route are completed before any pickups are made and the vehicle capacity is not violated by either the linehaul or backhaul points assigned to the route. The objective is to find such a set of routes that minimizes the total distance traveled. The primary contribution of this work is the development of an optimization based approach for the vehicle routing problem with backhauls, which is based on the Generalized Assignment Problem, and will be referred to as LHBH. In particular, a new algorithm based on angle location-allocation is used in the seed location step of the GAP algorithm. The LHBH algorithm can be applied to realistically sized problems, with results which can increase productivity and lower costs in the distribution of goods.
The algorithm is based on two additional assumptions. First, the distances traveled by the vehicles can be computed with sufficient accuracy as proportional to the Euclidean distance, i.e. proportional to straight-line distance. Second, the number of backhaul points is of the same order of magnitude as the number of linehaul points. We have not tested our algorithm for cases where the number of backhaul points is very small or when the customers are naturally clustered together, rather than uniformly distributed over the service region.
The importance of VRPB is related to the very large cost of physical distribution. In a report prepared for the National Council of Physical Distribution Management (NCPDM), Kearney (1984) estimates annual distribution costs in the United States in 1983 at $650 billion, approximately 21% of the GNP. In addition, Kearney reports that logistics costs account for 22.5% of the controllable costs in manufacturing. VRPB's significance can also be attributed to the continuing effort to reduce distribution costs by taking advantage of the unused capacity of an empty vehicle traveling back to the DC. The Interstate Commerce Commission News (1980) estimated the potential fuel savings of using backhauling to be 42 million gallons a year nationally. Kearney includes a summary of programs implemented by companies in the period from 1978-1983 for improving productivity in logistics. The number one program, utilized by 83% of the survey respondents, was coordination of inbound with outbound freight to provided private fleet backhauls.
In addition, government deregulation of interstate commerce restrictions in the Motor Carrier Act of 1980 has made it possible for backhauling to become a profitable venture for any company with a large fleet of vehicles. Commodities can now be backhauled not only for the owning company, but also for other companies who are willing to pay for the backhauls as though for common carriage. One company in Michigan increased its backhauling revenues from $697,000 to almost $2 million in just two distribution centers (Orr, 1989). Other companies which are utilizing backhauling to generate revenues include Frito-Lay, K Mart, and Friendly Ice Cream (Chancellor, 1988). Backhauling is truly emerging as an untapped resource for improved productivity in industry.
This paper is organized as follows. A literature review is given in Section 2, with some brief discussion of consideration for the addition of backhaul customers to the classical VRPB approaches. Also in section 2.0 some of our previously published background material is presented. Section 3 provides an explanation of the LHBH solution algorithm. The results of the computational study are detailed in Section 4, and in Section 5 conclusions are discussed.
Solution methodologies for the classical VRP include both exact and heuristic techniques. A comprehensive literature review can be found in Bodin et al., (1983) and many other studies in the area of vehicle routing have been reported in the years since. Golden and Assad (1988) provide an extensive review of the recent literature on vehicle routing. This section will describe how some of the methods for VRP could be adapted to VRPB, and report on current VRPB research.
The standard VRP can be thought of as a special case of VRPB, with the number of backhaul points equal to one (the distribution center). Since VRP is NP-complete (Lenstra and Rinnooy Kan, 1981), the VRP with backhauls is also NP-complete. The development of heuristic approaches is therefore a reasonable approach for practical applications. An exact procedure based on set covering was developed by Yano et al., (1987) for a special case of the VRPB. Relaxing the special route conditions or increasing the number of backhaul points would make this exact procedure computationally intractable. Gelinas (1991) also developed an exact procedure for the VRPB with time windows which will be discussed in more detail in Section 4.5.
The literature described here proposes ways to solve the backhaul routing problem based on some well-known methods for the classical VRP. The solution methodologies are categorized according to a scheme suggested by Bodin et al., (1983). In addition to solution methodologies, work has been done to develop planning models for incorporating backhaul loads into an existing transportation system. Jordan and Burns (1984) examined the impact of backhauling on terminal locations and developed a method for determining which truckloads should be backhauled. Jordan (1987) extended this work to include systems with more than two terminals.
Cluster-first/Route-second. This strategy is illustrated by the sweep algorithm of Gillett and Miller (1974). The sweep approach can easily be extended to the VRPB by truncating the clusters when either linehaul or backhaul capacity is exceeded.
Route-first/Cluster-second. Extension of this approach to VRPB can be accomplished by solving a Traveling Salesman Problem (TSP) for the delivery points, then solving a TSP for the pickup points. Each of the large tours can be broken up into individual delivery and pickup routes, which can then be patched together to form linehaul-backhaul routes. Goetschalckx and Jacobs (1989) investigated a similar approach based on spacefilling curves. This method is included in the experimental comparison in Section 4.
Savings/Insertion. This concept is a constructive approach whereby a configuration of points is changed to an alternative configuration which yields a 'savings' in terms of a particular objective. Perhaps the most widely known and used savings algorithm for the VRP was developed by Clarke and Wright (1964). Deif and Bodin (1984) have proposed an extension of this algorithm for VRPB. This modified Clarke-Wright method will be described in detail in section 4.1.
Golden et al., (1985) and Casco et al., (1988) report on an insertion procedure for VRPB where any VRP algorithm is used to initially sequence the delivery customers. Once the linehaul customers are routed, the backhaul customers are inserted onto the delivery routes according to an insertion criterion based on a penalty for pickup before the end of the delivery route. This is a relaxation of the linehaul-backhaul sequencing constraints. This approach is most applicable to the cases where there are very few backhaul points.
Improvement/Exchange. Perhaps the best known method is the r-opt algorithm of Lin and Kernighan (1973). Other exchange procedures exchange customers between routes, instead of within routes. Such methods can easily be applied to a given solution for VRPB by taking into account the precedence relationship of deliveries before pickups whenever an exchange is considered. Further discussion of these methods will be presented in section 4.3.
Optimization-Based Techniques. Min et al., (1992) develop a methodology for solving the VRPB when multiple depots are involved, denoted by MDVRPB. They use a decomposition approach, determining first the delivery/pickup clusters, then assigning those clusters to depots and routes, and finally the sequencing of the route itself. In determining the delivery/pickup clusters, they use a statistical clustering method to take advantage of the spatial nature of the problem. They claim that statistical clustering is computationally more efficient than mathematical programming clustering for large number of points. In the second step, delivery route, pickup route, and depot are assigned to each other by a three dimensional assignment formulation (3DAP). They solve only the linear relaxation for their example case. Finally, the linehaul-backhaul routes are constructed by an optimal asymmetrical TSP algorithm, after all the distances from pickup points to delivery points have been set to infinity. Their method is computationally efficient because, for their example, the 3DAP can be solved with linear programming and the number of points on the linehaul-backhaul routes is smaller than 19.
Two acclaimed approaches for VRP were presented by Fisher and Jaikumar (1978, 1981), and by Cullen et al., (1981) and Cullen (1984). The first approach is based on the Generalized Assignment Problem and the second on Set Partitioning. Desrochers et al., (1992) present a set partitioning algorithm for VRP with time windows (VRPTW) which can be used to find optimal solutions to the problem. Gelinas (1991) has extended this work for VRPB. There has apparently been no further published work to date on optimization-based heuristic methods for VRPB.
Goetschalckx and Jacobs-Blecha (1989) developed an integer programming formulation for the VRPB problem by extending the Fisher and Jaikumar (1981) formulation to include pickup points. The model naturally decomposes into three subproblems. The first two subproblems correspond to the clustering decisions for the delivery customers and the pickup customers, which are independent Generalized Assignment Problems (GAP). The third subproblem consists of K independent, single route TSPs, each having one additional constraint, enforcing the completion of all deliveries before any pickups can be made. These precedence constraints impose a dependency relationship on all the model components. This relationship is also indicative of the importance of the routing links adjoining delivery to pickup in each route. They develop an efficient and effective heuristic solution algorithm for this problem based on spacefilling curves. Some of the properties of the VRPB are discussed in the next section, which leads to the algorithm specification in Section 3.0.
Jacobs-Blecha (1987) showed that for Euclidean distances the VRPB routes will never be more expensive than executing separate delivery and pickup routes. The best savings occurs when the pickup and delivery customers are all collinear with the DC, and the pickup and delivery locations farthest from the DC are coincident. This example shows that the maximum savings achievable by backhauling is 50%, as opposed to sending a separate and independent truck for the backhauling.
Jacobs-Blecha (1987) also derived a worst case bound equal to 3 for the a simple heuristic for the VRPB by extending the results of Haimovich and Rinnooy Kan (1985) for the classical VRP, whose bound equals 2.

The fundamental structure of a VRPB route consists of three parts. The first is a Hamiltonian path from the DC through all delivery points, ending at the delivery interface point. The second component is the interface link between delivery and pickup customers. Third is a Hamiltonian path from the DC through all pickup points, terminating at the pickup interface point. The set of delivery customers on the delivery path comprises a sector of the plane anchored at the DC. A similar sector is defined by the set of pickup customers on the pickup path. Jacobs-Blecha (1987) showed that the best savings from backhauling can be attained by minimizing the angles of the delivery and pickup sectors as well as the angle between the delivery and pickup sectors, as shown in Figure 1. This property will be exploited in the initialization phase of the LHBH algorithm.
The algorithm LHBH is based on the Generalized Assignment Problem, and is similar to the Fisher and Jaikumar (1981) GAP heuristic for VRP. However, this method differs most from Fisher and Jaikumar's approach in two respects. LHBH employs a fresh, new method for executing the process known as route seeding. In addition, the LHBH route seeds are extended into unique, high quality route primitives by exploiting the properties described in Sections 2.3 and 2.4.
The algorithm comprises three phases:
In the initialization phase, an initial solution is obtained and costs are estimated for solving the clustering problem. In phase (2), the costs from (1) are used to solve the Generalized Assignment Problem, which allocates the delivery and pickup customers to a set of minimal cost routes. Phase (3) is concerned with solving the TSP for each cluster formed in (2), taking into account the precedence relationship described in section 2.3. The following sections will explain each of these steps in further detail.
The purpose of the initialization phase is to provide a set of approximate locations for the route clusters. Although the concept of route locations is somewhat nebulous, the spatial perspective of the problem suggests that customer proximity plays a strong part. From the route structure analysis, locations are sought which will tend to minimize the route sector angles and the angles between the delivery and pickup sectors. To locate the route clusters, the multifacility location model (see Francis and White, 1974) is utilized, viewing the demand (or pickup) points as existing facilities and the cluster locations as new facilities. This provides a fundamentally new way of initializing the Fisher and Jaikumar approach to vehicle routing problems.
In determining the location of the route clusters, the initialization phase begins by uniformly locating radials around the DC to represent each of the VRPB routes. In real-time, the dispatcher could physically place these initial radials based on known streets and roads. The location and distance between all pickup and delivery customers are computed using a distance metric based on angles, the ring-radial metric, as prescribed by the route structure analysis. The facility location problem is then solved iteratively as a capacitated location-allocation problem with the single sourcing constraints relaxed. This allows cluster determination to be influenced both by the spatial distribution and customer demand. This approach has the advantage of achieving good seed locations for both uniformly and clustered distributions of customer facilities.
The ring-radial metric (see Mittal and Palsule, 1984) is the distance
metric used in the facility location model. Figure 2 illustrates
this metric. Let 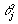
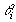
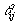
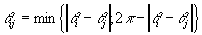
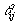 is used to measure the "distance" between a customer
and a route location. The solution to the problem yields a set
of angles that define the radials, along which each VRPB route
should be located. This set of radials serves as the route
seeds for the initial VRPB route locations. It is possible
for the customer allocations obtained in this initialization phase
to be infeasible with respect to single sourcing. However, only
the route locations are used in the next phase of the solution
procedure, and any such infeasibility is eliminated when the clustering
is completed.
is used to measure the "distance" between a customer
and a route location. The solution to the problem yields a set
of angles that define the radials, along which each VRPB route
should be located. This set of radials serves as the route
seeds for the initial VRPB route locations. It is possible
for the customer allocations obtained in this initialization phase
to be infeasible with respect to single sourcing. However, only
the route locations are used in the next phase of the solution
procedure, and any such infeasibility is eliminated when the clustering
is completed.

In the clustering step of algorithm LHBH there are two tasks to be accomplished: (1) determine the cost of assigning a customer to a route, and (2) use the costs to make the route assignments by solving the Generalized Assignment Problem.
Once the seed radials have been established in phase two, a route primitive is generated by choosing points for the route that are near the seed radial. (In this case, an angle "distance" of 10 degrees or less was considered "near"). For each route, linehaul points are sequenced by increasing distance to the distribution center and backhaul points by decreasing distance. Any point which is within 10 degrees of more than one seed radial is not placed in either primitive, and left unassigned. This assignment of points results in a polygonal route primitive from which the GAP costs can be determined. Such a set of route primitives is illustrated in Figure 3.

Once the route primitives are found, the Euclidean distance metric is used in the remainder of the clustering phase. For problems where customers are randomly located in the region around the DC, determining routes that fit the model of minimal sector angles is not likely to happen. In such cases, Euclidean distance is a better estimator of nearness than the ring-radial metric. In cases where customer locations are naturally clustered, the ring-radial metric would be a better choice. Since this study focuses on randomly located customers, in the following discussion the Euclidean metric is applied .
In LHBH, Martello and Toth's (1981) savings regret heuristic is implemented for solving the GAP. This method assigns points to routes in a sequential manner based on a computation of the regret to be experienced by waiting until later to make the assignment. Possible improvements to the resulting routes are sought with the application of a Lagrangean heuristic which will be described below.
The cost of assigning each remaining point i to route k is estimated as the minimum insertion cost of point i into the links of the primitive for route k. Since the savings regret heuristic is sequential in it assignments, each time a point is assigned to a route, the primitive for that route grows and the insertion costs for points yet to be assigned to that route may change. Thus, the cost estimates for assigning the remaining points to the growing route primitives change dynamically. It is a simple computational update to keep the costs current as the GAP is solved. This dynamic implementation of the savings regret method has been implemented in LHBH.
The GAPs for VRPB are solved in two stages. First, the dynamic sequential step builds a set of customer-route assignments based on the savings regret heuristic. Then, an improvement step is implemented by applying a Lagrangean heuristic developed by Jacobs (1987). This Lagrangean heuristic takes an initial set of dual multipliers, solves the Lagrangean to obtain a lower bound, adjusts the solution to feasibility to obtain an upper bound, adjusts the multipliers, and iterates. The procedure stops when either the difference between the upper and lower bounds is sufficiently close, or when a maximum number of iterations has been executed.
The sequencing problem consists of a TSP for each cluster with a side constraint restricting the tour to only one link from delivery to pickup. A practical solution method is to apply any construction heuristic followed by 2-opt and 3-opt. Golden et al., (1980) have shown this to be on average within 2% of optimality for the TSP which occurs in the classical VRP. Goetschalckx and Jacobs (1989) have confirmed this for the VRPB and have shown this to be the best tradeoff between tour length and computation time.
The best sequence of points for a cluster is highly dependent on the link selected as the interface between delivery and pickup. The heuristic for approximating the best sequence begins by determining a pair of artificial interface points. The cluster of delivery points geometrically defines a pie-shaped sector of the plane, anchored at the DC, (see Figure 4). The two "corner" points of this sector are candidates for the artificial delivery interface point. Similarly, there are two candidates for the artificial pickup interface point. The closest pair of candidate points, one from each sector, are selected as the initial interface points. Note that these points are artificial in the true sense of the word. It is likely that neither of them are actually located at a customer site. This selection of interface points creates an artificial interface link, joining the two sectors.

Using the artificial interface link as the base, the cheapest insertion procedure is performed to create an initial feasible tour for the route. At this point, the artificial interface points are discarded and the actual interface points for pickup and delivery point are designated as the current interface points. To allow the two sides of the route to interact with each other (as the mathematical model indicates is the case), two-opt and three-opt are performed in a special way.
The current pickup interface point is "added" to the delivery route and forced to remain as the final point to be visited by setting its distance to the DC = -. The two-opt and three-opt procedure is then performed on this set of points. Since the current delivery interface point is not restricted from being changed in the delivery route, the delivery interface point is then updated. This procedure is now performed for the pickup route, adding the current delivery interface point to the set, as before. The procedure then repeats until there is no further reduction in the cost of the route. This procedure converges quickly to an interface link which determines a good sequence for the overall VRPB route.
Algorithm LHBH can now be specified as follows:
1. Initialization. Find initial seed radials by solving the location-allocation problem, utilizing the ring-radial distance metric.
2. Clustering. Find polygonal route primitives from the current seed radials.
Assign the delivery and pickup points to the routes using a savings regret heuristic, dynamically re-estimating the GAP costs as the points are assigned. Attempt to improve the route clusters by applying a Lagrangean heuristic.
3. Routing. Heuristically solve the special TSP problem for each route by cheapest insertion, using an iterative technique to search for a good interface link. Apply two-opt and three-opt to the resulting routes.
4. Iteration. Using the ring-radial metric, locate a new set of seed radials from the current route clusters.
5. Convergence. If the seed radials are unchanged, or the maximum number of iterations has been executed, then stop. Otherwise, return to step 2.
To evaluate the efficiency and effectiveness of the LHBH heuristic, the algorithm is compared computationally with three other algorithms for solving the VRPB, providing results for both solution costs and execution times. For each of these alternative solution methods a description of the algorithm is given, along with further references. A discussion of exchange heuristics for improving a given solution is also presented. In addition, an exact algorithm and lower bound computation is provided as a solution quality benchmark for LHBH.
Clarke and Wright (1964) developed an algorithm for the vehicle
routing problem based on the computation of a savings for
combining two customers into the same route. Initially, each
customer is considered to be on a separate route. The savings
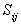
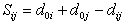
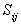 is computed for every pair of points
i and j and arranged in non-increasing
order.
is computed for every pair of points
i and j and arranged in non-increasing
order.
Deif and Bodin (1984) proposed an extension of this algorithm
in an effort to produce good solutions to the VRPB. Their procedure
is based on two modifications to the original Clarke-Wright algorithm.
The first modification adds the constraint that only one link
from delivery to pickup (or vice versa) is allowed on any route.
Second, the definition of savings is modified to include a penalty
to reduce the size of savings for a changeover from delivery to
pickup. The modified savings computation is:
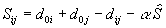
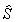 is an estimate of the maximum value of savings and
is an estimate of the maximum value of savings and 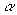 is a penalty multiplier. If i and
j are both delivery points,
or both pickup points, then
is a penalty multiplier. If i and
j are both delivery points,
or both pickup points, then 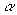 is 0.
The maximum savings is estimated by as an efficiency measure,
since the savings list grows as a quadratic function of the number
of customers. The penalty
is 0.
The maximum savings is estimated by as an efficiency measure,
since the savings list grows as a quadratic function of the number
of customers. The penalty 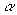 reduces
the size of the savings for a changeover from delivery to pickup.
reduces
the size of the savings for a changeover from delivery to pickup.
An alternative approach for solving the VRPB is to treat the problem as two separate VRP's, forming routes for the delivery points independently of the pickup points, and vice versa. A solution to VRPB can then be formed by simply patching the two sets of routes into a single set of routes by matching the delivery and pickup routes.
To solve the two separate routing problems, the Generalized Assignment heuristic method, introduced by Fisher and Jaikumar (1981) was selected, and will be referred to as ROVER. The ROVER algorithm is a benchmark that includes an exact GAP solution, developed by Fisher, Jaikumar, and Van Wassenhove (1986). Once the VRPs are solved, the VRPB solution is completed by pairing the delivery routes need with the pickup routes. This can be accomplished by solving a simple assignment problem with an appropriate definition of the cost of assigning a pickup route to a delivery route. Two approaches were developed.
The first approach is a simple one which is computationally inexpensive. For each pair of routes, only points adjacent to the depot on the separate routes are considered as candidates for interface points. This means that four pairs of delivery and pickup points are considered, and the one yielding the most savings in travel distance determines the candidate interface link and the assignment cost for that pair of routes. The cost matrix for the assignment problem is found by computing this savings for all pairs of routes from the VRP solutions. The VRPB algorithm incorporating this simple matching solution will be denoted by RVR.
The first method of computing the assignment costs clearly may not yield the best pairing, nor the best interface links for the resulting set of paired routes. To find the best set of interface links for two given sets of delivery and pickup routes, it is necessary to consider every delivery point with every pickup point as a candidate interface, for every pair of routes. For each of these candidates, a TSP solution must then be computed, and the total cost of the resulting routes compared. The TSP problems were solved by cheapest insertion followed by 2-opt and 3-opt. This time-consuming approach will be referred to as RVRBST.
The 2-opt and 3-opt heuristics have been applied to all heuristic solutions reported in this paper unless otherwise indicated. In applying the procedures to VRPB, the precedence restriction in the changeover from delivery to pickup was preserved.
The k-opt concept can be applied to sets of routes by removing customers from one route and inserting them into another for a savings in travel distance. There are two ways in which this exchange procedure was applied to the problems in this paper:
Bartholdi et al., (1983) introduced the idea of using spacefilling curves to develop heuristics for routing problems. The spacefilling curve/routing concept is essentially to reduce the planar problem to a linear problem, and then to take advantage of the geometric relationship between the two problems. The advantages of these heuristics are their ease of execution and their speed, in addition to a fairly good solution quality. Goetschalckx and Jacobs-Blecha (1989) developed heuristics for the VRPB based on the concept of spacefilling curves. The spacefilling curve solutions will be referred to as Spcfill.
The VRP and also the VRPB can be formulated as a Set Partitioning Problem (SPP) with a constraint set insuring each customer is visited. This problem has a large number of columns, each corresponding to a single route. If the integrality constraints of the SPP are relaxed, the resulting linear program (LSPP) can be solved and dual variables associated with each customer. A new route (or column) can be evaluated with these dual variables. A subprocedure is responsible for generating columns with a negative reduced cost and these are added to the LSPP. The LSPP is then resolved and the procedure iterates until no further negative reduced cost columns can be found. If the solution is not integer it provides a lower bound to the VRPB. This lower bound can then be used in a branch-and-bound algorithm. A detailed discussion of this technique is given in Desrochers et al., (1992).
Gelinas (1991) has used this method to solve a wide variety of VRPB problems with time windows for up to a 100 customers. The route generator is a shortest path on a network with vehicle capacity constraints as described in Desrochers (1988). With wide or relaxed time window constraints the problem becomes more difficult to solve because of a large integrality gap. In the computational study of our test problems by Gelinas and Desrochers (1991), only problems of size 30 (total customers) or less could be solved to optimality, since the time windows were totally relaxed. For problem sizes up to 94 customers a lower bound was obtained based on the LSPP, which will be referred to as LoBnd.
For ease of reference the list of heuristics and their abbreviated names are given in Table 1.
All test problems were randomly generated, with pickup and delivery
point locations uniformly distributed in a rectangular service
region. For both sets of customers, x-coordinates were generated
over the interval (0,24000), and y-coordinates over the interval
(0, 32000). The depot was centrally placed at (12000, 16000)
for all test problems (the coordinate bounds for the customer locations
were simply based on the limits of the video screen). Demand and supply
data was selected from a normal distribution with a mean of 500
units and standard deviation of 200 units. This data set is summarized
in Table 2, presenting the problem description for each of the
63 test problems. ASCII files containing actual customer coordinates
and demand quantities can be obtained from the authors.
| Problem | Problem | |||||||
| Group | Group | |||||||
| A | H | |||||||
| 20 dels | 45 dels | |||||||
| 5 pkups | 23 pkups | |||||||
| I | ||||||||
| B | 45 dels | |||||||
| 20 dels | 45 pkups | |||||||
| 10 pkups | ||||||||
| C | ||||||||
| 20 dels | J | |||||||
| 20 pkups | 75 dels | |||||||
| 19 pkups | ||||||||
| D | ||||||||
| 30 dels | K | |||||||
| 8 pkups | 75 dels | |||||||
| 38 pkups | ||||||||
| E | ||||||||
| 30 dels | L | |||||||
| 15 pkups | 75 dels | |||||||
| F | 75 pkups | |||||||
| 30 dels | ||||||||
| 30 pkups | ||||||||
| M | ||||||||
| G | 100 dels | |||||||
| 45 dels | 25 pkups | |||||||
| 12 pkups | ||||||||
| N | ||||||||
| 100 dels | ||||||||
| 50 pkups | ||||||||
| H | ||||||||
| 45 dels | ||||||||
| 23 pkups |
All heuristic procedures discussed in this paper were coded in Microsoft Pascal and executed on a 20 MHz 386-based PC with math coprocessor. Execution times are reported in CPU seconds for this machine. Table 3 provides a summary of the results of the solutions from each of the eight procedures, including the results of LHBH and CW both before and after the 2-opt and 3-opt procedures. Reported is the average total distance for all solutions of a particular problem size. No results are indicated for Swappair or Swappoint since, when applied to the results after 2- and 3-opt had been executed, no significant improvement was produced.
|
|
|
|
|
|
|
|
|
pre-opt indicates the results obtained before 2-opt and 3-opt were performed.
* indicates solutions could not be obtained in the allotted amount of time
In Table 4, data is presented which shows the percentage improvement of the LHBH algorithm over the other heuristic methods in terms of total solution cost. Note that results for the Clarke-Wright algorithm are presented both before and after 2-opt and 3-opt and the pre-improvement LHBH solutions are also included.
It is obvious that both Rover and the Spacefilling Curve method
are inferior to LHBH. The average improvement of LHBH over RVRBST
was 20%, with a maximum improvement of 50% (for an individual
case). The Spacefilling Curve heuristic performed only slightly
better with an average improvement by LHBH of 19%, and a maximum
of 38% (for an individual case). The poor performance of these
methodologies can easily be attributed to their nature. Both
methods solve the problem with a disjunctive approach. The two
routing problems are solved independently of each other, and the
results are integrated without appropriate information on how
the two problems interact.
|
|
|
| |||
| 0.00% | 1.30% | 1.44% | 22.13% | 23.72% | 16.90% | |
| 1.94% | 6.14% | 4.75% | 22.56% | 27.02% | 20.35% | |
| 0.00% | 2.81% | 2.47% | 4.70% | 6.90% | 9.67% | |
| 2.20% | 1.23% | 0.94% | 7.59% | 16.89% | 16.86% | |
| 1.59% | -0.48% | -0.51% | 24.57% | 23.87% | 24.03% | |
| 0.33% | 1.39% | 0.73% | 15.36% | 22.06% | 21.24% | |
| 3.30% | 4.34% | 1.96% | 15.08% | 26.04% | 16.10% | |
| 1.55% | 5.40% | 4.96% | 36.83% | 43.80% | 23.71% | |
| 0.56% | 0.80% | 0.52% | 26.09% | 35.15% | 19.49% | |
| 2.15% | 1.30% | 0.37% | 14.80% | |||
| 0.41% | 4.43% | 3.63% | 15.32% | |||
| 0.82% | 4.20% | 2.95% | 16.58% | |||
| 1.16% | 7.05% | 5.62% | 28.81% | 41.16% | 23.92% |
From the data presented in Tables 3 and 4, it is not obvious that LHBH is a better algorithm than CW. The performance of LHBH is not significantly better than the Clarke-Wright savings heuristic in terms of total distance traveled. The average improvement was approximately 3% with a maximum of 11% (for an individual case). Moreover, in 20 of the 63 problems the solution values were essentially equivalent. However, it should be noted that LHBH has other qualitative performance characteristics that are not easily measured in a quantitative way. Some of these characteristics have been observed through a graphical user interface which was built into the experimental model.
Perhaps one of the most ineffective characteristics of the Clarke-Wright method is its lack of flexibility. The number of routes produced by CW is not user-defined, nor controllable at all, as it is in LHBH. This means that CW produces the smallest number of routes into which the customers will feasibly fit. While this indicates high vehicle utilization in ideal operational settings, real-time problems may arise where this impact is undesirable. For example, a dispatcher may require additional routes to be used, or space may be needed on some of the vehicles for some other purposes. In addition, there is no flexibility in choosing the locations of the routes. While a very good procedure for locating routes has been provided in LHBH, CW permits no such input. In addition, a user-interactive route location feature could easily be added to LHBH to provide even more flexibility, where this could only be done in the CW environment after the solution was complete.
A second, unsatisfactory feature of CW is the architecture of the routes it produces. The fundamental nature of the algorithm tends to cluster points on the periphery of the service region, creating long circuitous routes with lengthy travel to and from the depot. Since backhauling is looked upon as a means of minimizing deadhead travel, this implies such routes will not be favored by dispatchers. The customers near the depot are then left to be assigned by CW to routes which sometimes nearly circle the depot. Allotting to drivers routes of such different characteristics can create additional personnel problems. LHBH routes, on the other hand, tend to lie in a more clearly defined sector of the plane and interroute distances differ modestly. These routes are intuitively appealing to the eye, and dispatchers can easily make changes to the routes as real-time problems arise.
A second measure of performance is the efficiency of an algorithm, i.e., how quickly can solutions be found and how does this execution time compare to other methods? Table 5 lists the average execution time for the various problem sizes and provides a comparison of the solution times for each of the heuristics. Based on the solution quality results discussed above, the real competitor to LHBH is the CW algorithm. However, the times given are in CPU seconds, and the maximum average time is less than three minutes for LHBH, for a 150 customer problem. With more powerful computing workstations now available, all of these algorithms could be competitively executed in real time, with little significance being placed on the differences in execution time.
LHBH is never more than 10% from the lower bound (with the exception of one problem) for this difficult-to-solve set of problems. These results indicate LHBH to be a viable algorithm for solving realistically sized VRPBs when customers are uniformly distributed. The procedure to find initial seed radials works well for clustered as well as uniformly distributed customers, because it iterates between location of routes and allocation of customers. Thus, the LHBH algorithm is expected to show the same high quality performance for clustered customers.
| 25 | 7.75 | 6.50 | 0.61 | 0.43 | 1.17 | 2.36 | 2.81 |
| 30 | 5.67 | 4.67 | 0.73 | 0.55 | 3.22 | 2.39 | 3.06 |
| 38 | 18.00 | 17.00 | 2.07 | 2.00 | 2.89 | 1286.72 | 3.89 |
| 40 | 9.75 | 8.25 | 1.57 | 1.35 | 4.26 | 3.23 | 3.59 |
| 45 | 17.67 | 14.00 | 2.39 | 2.10 | 13.38 | 5.22 | 2.89 |
| 57 | 25.17 | 18.67 | 6.25 | 5.86 | 27.57 | 10425 | 5.12 |
| 58 | 32.67 | 20.67 | 6.40 | 5.77 | 60.47 | 8.15 | 6.38 |
| 60 | 32.50 | 27.50 | 6.37 | 6.04 | 27.92 | 36.47 | 4.66 |
| 90 | 42.40 | 33.80 | 18.51 | 17.92 | 106.41 | 5703.79 | 10.29 |
| 94 | 74.25 | 59.25 | 23.28 | 22.50 | 9.26 | ||
| 113 | 99.75 | 82.50 | 64.19 | 63.39 | 9.11 | ||
| 125 | 157.25 | 127.75 | 79.45 | 77.95 | 16.09 | ||
| 150 | 159.00 | 126.00 | 130.75 | 129.06 | 644.66 | 717.93 | 18.18 |

The Vehicle Routing Problem with Backhauls is a very important and present-day problem, impacting costs and productivity in industrial distribution systems. Like many other routing problems, the VRPB is a complex problem and heuristic algorithms are required to obtain solutions in a reasonable amount of time for realistic problem sizes. The heuristic approach introduced in this paper, LHBH, introduces a route seeding procedure based on angles, and a GAP solution with dynamically updated costs. Solution times for this algorithm are quite modest: no more than three minutes for a 100 by 100 customer problem on a relatively slow microcomputer. With the more powerful workstations that have become available since this work was completed, LHBH would likely produce solutions well within acceptable limits of dispatching operations.
LHBH was compared with other solution methods. It was shown that LHBH performed no worse that the savings approach in terms of solution time and quality. However, there are several qualitative benefits from using LHBH that cannot be acquired in the savings algorithm, namely solution flexibility and the fundamental nature of the route structure. LHBH performed significantly better than the spacefilling curve heuristic and the sequential VRP approach, LHBH was also compared to optimal/lower bound solutions from an exact algorithm. The results indicate LHBH can produce solutions which are less than or equal to ten percent of the mathematically optimal solution.
In summary, the computational study has shown LHBH to a viable heuristic for the VRPB with an excellent overall solution quality, and small computing times. LHBH produces routes which are flexible. This allows the user to interactively make modifications to the solutions needed to react to real-time needs.
Future extensions to this work could include time windows. Much work on this topic has already been done for the VRP, and will be useful in the study of the VRPB with time windows. The result should be a very versatile and accurate algorithm for the vehicle routing problem with backhauls and time windows.
This work was supported by the member companies of the Material Handling Research Center at Georgia Tech.
We wish to thank Martin Desrochers and Sylvie Gelinas of the Department de Mathematiques Appliquees University of Montreal for developing the lower bound, and computing it for our test cases. Without their work the evaluation of the quality of the LHBH algorithm would not have been complete.
Many thanks are due to Professor Van Wassenhove, then at the Catholic University of Leuven, Belgium, and now at the INSEAD in Paris, France, for supplying the FORTRAN code for the ROVER algorithm.
Bartholdi, J. J., L. K. Platzman, R. L. Collins, and W. H. Warden (1983), "A Minimal Technology Routing System for Meals-on-Wheels," Interfaces, Vol. 13, No. 3, pp. 1-8.
Bodin, L. D., B. L. Golden, A. A. Assad, and M. O. Ball (1983), Computers and Operations Research, Special Issue on the Routing and Scheduling of Vehicles and Crews, Vol. 10, No. 2, pp. 63-211.
Casco, D. O., B. L. Golden, and E. A. Wasil (1988), "Vehicle Routing with Backhauls: Models, Algorithms, and Case Studies," in Golden and Assad (eds.), Vehicle Routing: Methods and Studies, pp 127-147.
Chancellor, A. (1988), "Snack Food Companies Haul More Than Chips," The Journal of Commerce and Commercial, March 21 edition, p. 1A.
Clarke, G. and J. Wright (1964), "Scheduling of Vehicles From a Central Depot to A Number of Delivery Points," Operations Research, Vol. 12, pp. 568-581.
Cullen, F. H. (1984), "Set Partitioning Based Heuristics For Interactive Routing," Unpublished Doctoral Dissertation, School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia.
Cullen, F. H., J. J. Jarvis, and H. D. Ratliff (1981), "Set Partitioning Based Heuristics for Interactive Routing," Networks, Vol. 11, No. 2, pp. 125-143.
Deif, I. and L. Bodin (1984), "Extension of the Clarke and Wright Algorithm For Solving the Vehicle Routing Problem With Backhauling," Proceedings of the Babson Conference on Software Uses in Transportation and Logistics Management, A. E. Kidder, Editor, Babson Park, MA, pp. 75-96.
Desrochers, M., Desrosiers, J. and M. Solomon, (1992). "A New Optimization Algorithm for the Vehicle Routing Problem with Time Windows." Operations Research, Vol. 40, No. 2, pp. 342-354.
Desrochers, M., (1988). "An Algorithm for the Shortest Path Problem with Resource Constraints", GERAD Technical Report G-88-27, Ecole des Hautes Etudes Commerciales, Montreal.
Fisher, M. L. and R. Jaikumar (1978), "A Decomposition Algorithm for Large-scale Vehicle Routing," Working Paper 78-11-05, Wharton Department of Decision Sciences, University of Pennsylvania.
Fisher, M. L. and R. Jaikumar (1981), "A Generalized Assignment Heuristic for Vehicle Routing," Networks, Vol. 11, No. 2, pp. 109-124.
Fisher, M. L., R. Jaikumar, and L. Van Wassenhove (1986), "A Multiplier Adjustment Method for the Generalized Assignment Problem," Management Science, Vol. 32, No. 9, pp. 1095-1103.
Francis, R. L. and J. A. White (1974), Facility Layout and Location, Prentice-Hall Inc., Englewood Cliffs, New Jersey.
Gelinas, S., (1991). "Fabrication de Tournees avec Rechargement" (in French, Construction of Backhaul Routes). Unpublished Master's Thesis, Ecole Polytechnique, Montreal.
Gelinas, S. and M. Desrochers, (1991), Personal communication.
Gillett, B. and L. Miller (1974), "A Heuristic Algorithm For the Vehicle Dispatch Problem," Operations Research, Vol. 22, pp.340-349.
Goetschalckx, M. and C. Jacobs-Blecha (1989), "The Vehicle Routing Problem With Backhauls," European Journal of Operational Research, Vol. 42, pp. 39-51.
Golden, B. L. and A. A. Assad Eds., (1988). Vehicle Routing: Methods and Studies. Elsevier Science Publishers, New York, New York.
Golden, B. L., E. K. Baker, J. L. Alfaro, and J. R. Schaffer (1985), "The Vehicle Routing Problem With Backhauling: Two Approaches," Working Paper Series MS/S 85-037, College of Business and Management, University of Maryland.
Golden, B., L. Bodin, T. Doyle, and W. Stewart, Jr. (1980), "Approximate Traveling Salesman Algorithms," Operations Research, Vol. 28, No. 3, Part II, pp. 694-711.
Haimovich, M., and A. H. G. Rinnooy Kan (1985), "Bounds and Heuristics for Capacitated Routing Problems," Mathematics of Operations Research, Vol. 10, No. 4, pp. 527-542.
Jacobs, C. D. (1987), "The Vehicle Routing Problem With Backhauls," Unpublished Doctoral Dissertation, School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia.
Jordan, W. C. and L. D. Burns (1984), "Truck Backhauling on Two Terminal Networks," Transportation Research-B, Vol. 18B, No. 6, pp. 487-503.
Jordan, W. C. (1987), "Truck Backhauling on Networks With Many Terminals," Transportation Research-B, Vol. 21B, No. 3, pp. 183-193.
Kearney, A. T., Inc. (1984), Measuring and Improving Productivity in Physical Distribution, A report prepared for the National Council of Physical Distribution Management, NCPDM, Oak Brook, IL.
Lenstra, J. K. and A. H. G. Rinnooy Kan (1981), "Complexity of Vehicle Routing and Scheduling Problems," Networks, Vol. 11, No. 2, pp. 221-227.
Lin S., and B. Kernighan (1973), "An Effective Heuristic Algorithm for the Traveling Salesman Problem," Operations Research, Vol. 21, pp. 498-516.
Martello, S. and P. Toth (1981), "An Algorithm for the Generalized Assignment Problem," Operational Research '81, J. P. Brans, Ed., North-Holland Publishing Co.
Min, H., J. Current, and D. Schilling (1992), "The Multiple Depot Vehicle Routing Problem With Backhauling," Journal of Business Logistics, Vol. 13, No. 1, pp. 259-288.
Mittal, A. K., and V. Palsule (1984), "Facilities Location with Ring Radial Distances," IIE Transactions, Vol. 16, No. 1, pp. 59-64.
Orr, A. (1989), "Spartan Looks Down the Road," U. S. Distribution Journal, February, pp. 43-48.
Yano, C. A., T. J. Chan, L. Richter, T. Culter, K. G. Murty, and D. McGettigan (1987), "Vehicle Routing at Quality Stores," Interfaces, Vol. 17, No. 2, pp. 52-63.