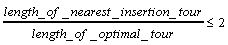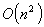TRAVELING SALESMAN PROBLEM
Insertion Algorithms

An insertion procedure takes a sub-tour on k nodes at iteration k and determines which of the remaining n-k nodes shall be inserted to the sub-tour next (the selection step) and where (between which two nodes) it should be inserted (the insertion step).

Nearest Insertion

• Step 1. Start with a sub-graph consisting of node i only.
• Step 2. Find node r such that c_ir is minimal and form sub-tour i-r-i.
• Step 3. (Selection step) Given a sub-tour, find node r not in the sub-tour closest to any node j in the sub-tour; i.e. with minimal c_rj
• Step 4. (Insertion step) Find the arc (i, j) in the sub-tour which minimizes c_ir + c_rj - c_ij . Insert r between i and j.
• Step 5. If all the nodes are added to the tour, stop. Else go to step 3

Worst Case Behavior:

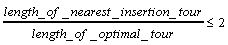
Number of Computations:

The nearest insertion algorithm is algorithm is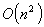.