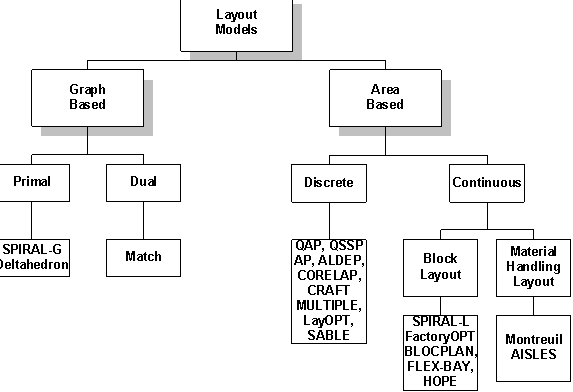



The theoretical layout models and their solution algorithms can be classified and organized based upon the properties shown in Figure 4.2. Graph based models generate an adjacency graph, while area based models generate a conceptual block layout. Primal models maintain a feasible solution while attempting to obtain an optimal solution. Dual models maintain an optimal solution while attempting to obtain a feasible solution. In discrete area models the departments and building are composed of a number of equal sized unit squares. In continuous area models the dimensions of the building and departments can have fractional values.

Figure 4.2. Theoretical Layout Models Hierarchy
The completed block layout can be represented as a graph. Similarly, the original relationship matrix can be represented as a complete undirected graph, where each department corresponds to a node and pairwise relationships form the edges. The adjacency graph is constructed from the relationship diagram by deleting all edges between non-adjacent departments, i.e. an edge is included in the adjacency graph if and only if the two departments are adjacent. The adjacency graph is thus a subgraph of the relationship diagram.
The block layout graph and the adjacency graph are related, in fact they are dual graphs. The relationship diagram can be constructed from the block layout by placing a node inside each department and by drawing the connecting relationship edge if and only if the two departments are adjacent, i.e. have a common wall. The resulting adjacency graph is planar. A graph is planar if it can be drawn in a two-dimensional plane without crossing edges.
From an adjacency graph a block layout can be constructed if and only if the adjacency graph is planar, see Seppanen and Moore (1970). The concepts of layout graph, adjacency graph and their dual relationship are shown in Figure 4.3.
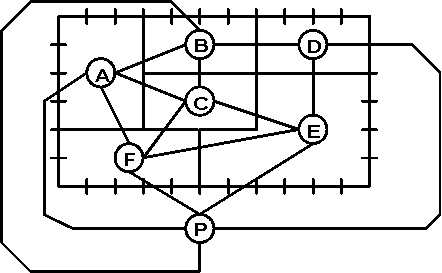
Figure 4.3. Adjacency Graph and Layout as Dual Graphs
The graph theoretic models are concerned with determining the best relative location of departments, ignoring the complexities of department and building shape and area. Their objective is to maximize the adjacency score. But in order to construct a block layout, the adjacency graph must be planar. Hence the problem is to extract a planar subgraph out of the relationship diagram, so that its edge weight is maximized and the graph is planar. This problem is called the Maximum (Weight) Planar Subgraph Problem (MPSP). This problem is NP-Complete and cannot be solved for practical problem size in reasonable amount of computer time.
