



The SPIRAL algorithm grows the relationship diagram in a crystalline, spiraling fashion. The original, manual form of this algorithm was first mentioned in Reed (1967). It relied completely on the insight of the engineer. A more sophisticated version that incorporates relationships with the outside, neighborhood improvement steps, and is based on hexagonal graphs is given in Goetschalckx (1986, 1992).
The SPIRAL technique constructs a guaranteed planar graph with high adjacency score based on an underlying hexagonal grid. The hexagonal grid where each department has six neighboring departments is illustrated in Figure 4.4. A typical adjacency graph created by SPIRAL is shown in Figure 4.5.

Figure 4.4. Hexagonal Grid Illustration
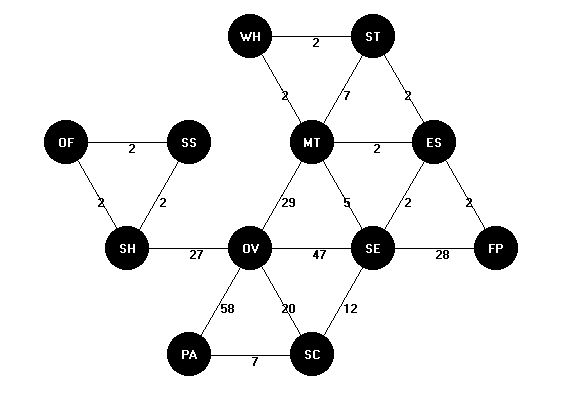
Figure 4.5. SPIRAL Adjacency Graph Illustration
The objective is to maximize the adjacency score based on a qualitative or numerical relationship chart. Departments are represented by standard, size independent symbols such as squares or circles. The data requirements are either a qualitative letter or quantitative relationship chart. The SPIRAL algorithm is one of the manual techniques to construct an adjacency graph or relationship diagram based upon a quantitative relationship matrix or flow matrix. The SPIRAL technique grows the graph in a crystalline manner by adding the department, which has the highest adjusted relationship, next to the graph so that the graph adjacency score is maximized. As such the manual SPIRAL algorithm is an example of a greedy, heuristic construction procedure.
In the first phase, the SPIRAL technique attempts to construct a good relationship diagram. The quality of the relationship diagram is measured by the adjacency score. Hence, the objective is to maximize the positive flow or relationships between adjacent departments and to minimize the negative flow or relationships between adjacent departments. Observe that later on the objective is to minimize the shape adjusted distance score of the final block layout.
Departments are entered in the hexagonal adjacency graph based on their adjusted relationship. The relationship tuple indicates on how many departments the adjusted relationship is based. Possible options are null, unary, binary, and ternary. The departments then enter the graph by decreasing adjusted relationship. The null tuple indicates that the next department will be chosen at random, without any regard to its relationships with other departments. The unary adjusted relationship sums the relationships of a department with all other departments. The binary adjusted relationship is the relationship between the current department and one other department. The ternary adjusted relationship is the relationship between the current department and two other departments.
Next, the relationships with the outside are incorporated. A department with a high positive spiral relationships will tend to be located early on in the procedure and hence on the inside of the graph. Similarly, a department with a small positive or a negative spiral relationship will tend to be located late and hence towards the perimeter of the graph. To incorporate the relationships with the outside in a consistent manner each spiral relationship is adjusted by subtracting the relationship of the departments in the tuple with the outside. For example, the adjusted unary, binary, and ternary spiral relationship (denoted by the subscript adj) are computed from the original relationships in the relationship matrix (denoted by the subscript orig) as:
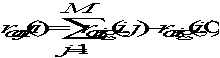 (4.1)
(4.1)
 (4.2)
(4.2)
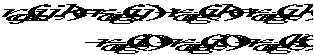 (4.3)
(4.3)
M is the total number of departments in the layout and 0 indicates the artificial outside department.
After the original graph is constructed three possible improvement steps can be executed. The options are none, two exchange, and three exchange. None does not execute an improvement step. Two exchange attempts to improve the graph in a steepest descent manner by attempting two department exchanges. It computes the savings generated by removing two departments out of the graph and swapping their position. The savings are based on an increase in the adjacency score. The exchange with the largest savings among all possible combinations of two departments is determined and if these savings are positive then those two departments are exchanged. The process repeats until no further improvements can be made. Three exchange attempts to improve the graph in a steepest descent manner by attempting three department exchanges. It computes the savings generated by removing three departments out of the graph and swapping their position. The savings are based on an increase in the adjacency score. The exchange with the largest savings among all possible combinations of three departments is determined and if these savings are positive then those three departments are exchanged. The process repeats until no further improvements can be made. Computational processing time increases sharply with the amount of improvement processing.
When locating a department in the partial adjacency graph often alternative positions are possible. Two possible tie breaker rules can be used. The first one is random which places the department randomly in one of the alternative positions based on a random number. The second one is centroid seeking which places the department in the position closed to the centroid of the current (partial) adjacency graph. If there are still alternative positions after the first tie breaker then a position is chosen at random. For further information see Goetschalckx (1992).
In the case of the hexagonal grid, an upper bound on the adjacency score of the graph can be computed based on the following integer programming formulation, where o (zero) represents the artificial outside department:
Max. 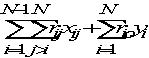 (4.4)
(4.4)
s.t. 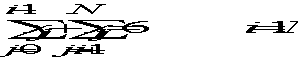 (4.5)
(4.5)
 (4.6)
(4.6)
 (4.7)
(4.7)
 (4.8)
(4.8)
 (4.9)
(4.9)
 (4.10)
(4.10)
The following notation is used: 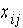 is 1 if departments i and j are adjacent, 0 otherwise. For the artificial outside department {
is 1 if departments i and j are adjacent, 0 otherwise. For the artificial outside department {
The formulation maximizes the adjacencies between departments and between a department and the outside (4.2), subject to the constraint that each department must have exactly six neighbors (4
The following notation is used: 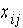 is 1 if departments i and j are adjacent, 0 otherwise. For the artificial outside department { is the binary
relationship between departments i and j..3). These neighboring departments can be the artificial outside department. If a department has at least one outside department as a
neighbor the relationship with the outside is satisfied and included in the objective function (4.4) and (4.5). All the adjacencies are binary variables, except the adjacencies with the outside
department which are linear (4.6), (4.7) and (4.8).
is 1 if departments i and j are adjacent, 0 otherwise. For the artificial outside department { is the binary
relationship between departments i and j..3). These neighboring departments can be the artificial outside department. If a department has at least one outside department as a
neighbor the relationship with the outside is satisfied and included in the objective function (4.4) and (4.5). All the adjacencies are binary variables, except the adjacencies with the outside
department which are linear (4.6), (4.7) and (4.8).
The value of the formulation lies in the fact that it provides bound on the optimal solution quality and on the maximum deviation of the heuristic solutions. The value returned by the algorithm in SPIRAL is the solution of the linear relaxation of the above formulation. In a linear relaxation all variables that originally were restricted to be either zero or one now can take any value between zero and one. In other words:
s.t.  (4.11)
(4.11)
 (4.12)
(4.12)
For more information see:
To Create a Hexagonal Adjacency Graph
To Compute an Upper Bound on the Graph Adjacency Score
