In the second phase, SPIRAL converts the hexagonal adjacency graph into a rectangular block layout. The building has to be rectangular and all department shapes will also be rectangular. SPIRAL constructs the block layout based upon layers. Each layer corresponds to all departments on an axis of the hexagonal adjacency graph. Once the departments in a layer are determined, the area of this layer and the shape of each department in the layer can be computed. The SPIRAL algorithm attempts to improve the resulting block layout by using two and three department interchanges.
Building Orientation
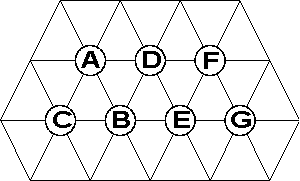
The building orientation indicates to which of the possible three axes of the adjacency graph the building width dimension is parallel. The adjacency graph has three main axes, horizontal or level, 60 degrees upward, and 60 degrees downwards of the horizontal level. The block layout construction algorithms will create a layout by putting departments in rows, where the rows are parallel to the building width dimension. Departments whose positions in the adjacency graph are on the same axis will be placed in the same row in the block layout.
Figure 4.6. Main Axes of Adjancency Graph
Layout Improvement
After the original block layout is constructed four possible improvement steps can be executed. The options are none, steepest descent exchange and annealing exchange. Each exchange improvement procedure can be based either on exchanging two or three departments at a time.
None does not execute an improvement step.
Steepest Descent exchange attempts to improve the graph in deterministic and greedy manner by attempting two or three department exchanges. The exchange with the largest savings among all possible combinations of two or three departments is determined and if these savings are positive then those two or three departments are exchanged. The process repeats until no further improvements can be made.
Two Exchange attempts to improve the layout in a steepest descent manner by attempting two department exchanges. It computes the savings generated by removing two departments out of the graph and swapping their position. The savings are based on a decrease in the shape adjusted distance score. Three Exchange attempts to improve the graph in a steepest descent manner by attempting three department exchanges. It computes the savings generated by removing three departments out of the graph and swapping their position. The savings are based on a decrease in the shape adjusted distance score.
Annealing Exchange attempts to improve the graph in stochastic, non steepest descent manner by attempting two or three department exchanges. There exists an analogy between the optimization method of simulated annealing and the laws of thermodynamics, specifically with the way in which liquids freeze and crystallize or metals cool and anneal. The algorithm computes the savings generated by removing three departments out of the graph and swapping their position. The savings are denoted by S. The savings are based on a decrease in the shape adjusted distance score. The three departments are chosen at random. If the savings are positive then the exchange is made. If the savings are negative, i.e. the distance score after the exchange is higher, then the exchange can still be made with a certain probability depending on the how long the simulated annealing algorithm has been executing. This time by convention is called the temperature of the annealing process and is denoted by T. The probability of an exchange based on savings S, denoted by P(S) is then computed as:
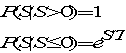(4.13)
During the algorithm execution the temperature T is systematically reduced. This allows early on exchanges with large negative savings. As the temperature is lowered, the number of such exchanges and the size of the allowed negative savings are gradually reduced. The objective of these non-improving exchanges is to avoid a steepest descent into a local minimum. The process repeats until no further improvements can be made.
For further information on two and three exchanges see Goetschalckx (1992). For further information on simulated annealing see Kirkpatrick et al. (1983) and Vechi and Kirkpatrick (1983).
Computational processing time increases sharply with the amount of improvement processing.
Space Allocation
The Layered space allocation method divides the building area in strips or layers parallel to the orientation of the building. All departments located on an axis of the hexagonal adjacency graph parallel to the building orientation are assigned to a single layer. The algorithm then assigns department areas from left to right in each layer. The Layered method has the advantage that it creates natural material handling aisles in the building.
The Tiled space allocation method divides the building area into a set of non-overlapping rectangular departments. The position of the department rectangles is derived from the hexagonal adjacency graph. The Tiled space allocation method recursively divides a partial building area along all possible vertical and horizontal rows and columns of the hexagonal adjacency graph and keeps the best layout generated so far. The Tiled space allocation method has more flexibility than the Layered space allocation method and on the average will yield layouts with a lower distance score. However, the resulting layout may not have the structure that aligns departments along parallel material handling aisles.
The Tiled space allocation method will always generate layouts with a score that is not larger than the score of layouts generated with the Layered space allocation method if no improvement exchanges are allowed. Because the improvement exchanges are heuristic algorithms, the Layered method may generate a layout with lower distance score than the Tiled space allocation method for individual project instances. Because the Tiled method examines many more alternatives than the Layered method, it requires substantially longer computation times.
For more information see:
To Evaluate the Current Graph and Layout