Some combinatorial applications of spacefilling curves

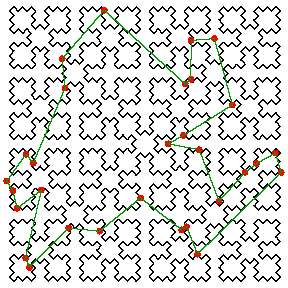
The spacefilling curve suggests a heuristic tour of a set of points

Figure 1: A heuristic solution to the Traveling Salesman Problem is to visit the points in the same sequence as the Sierpinski spacefilling curve.

A spacefilling curve is a continuous mapping from a lower-dimensional space into a higher-dimensional one. A famous spacefilling curve is that due to Sierpinski, which is formed by repeatedly copying and shrinking a simple pattern (the convoluted tour in Figure 1).

A useful property of a spacefilling curve is that it tends to visit all the points in a region once it has entered that region. Thus points that are close together in the plane will tend to be close together in appearance along the curve.

This forms the basis of the heuristic, invented by L. Platzman and me, to produce a reasonably short tour of n given locations (the so-called Travelling Salesman's Tour): Simply visit them in the same sequence as does the spacefilling curve. For example, a short tour of the points marked in read is indicated by the green lines, which connect the points in the same sequence as their appearance on the spacefilling curve.

The spacefilling curve heuristic (SFC) has many advantages, if you are willing to accept solutions that are about 25% longer than optimum (expected, for random point sets). These advantages include:

The SFC algorithm is fast: Only O(n log n) effort to construct a tour of n points and only O(log n) effort to update the solution by adding or removing points.
The SFC heuristic does not need explicit distances between points and so there is no need to compute or measure these, as most other heuristics must.
The algorithm is parallelizable. (In comparison, the comparable algorithm, Nearest Neighbor, is apparently not parallelizable.)
The length of links in the SFC tour of random points is expected to be small and of small variance, so that (1/k)-th of the stops account for about (1/k)-th of the travel time. This means that an SFC tour can easily be converted to tours for k vehicles simply by partitioning the SFC route into k segments.

The spacefilling curve heuristic has been used in many applications, including:

To build a routing system for Meals-on-Wheels in Fulton County (Atlanta, GA), which delivers hundreds of meals daily to those too ill or old to shop for themselves. We built this on two rolodex card files.
To route blood delivery by the American Red Cross to hospitals in the Atlanta metropolitan area.
To target a space-based laser for the Strategic Defense Iniative (commonly known as the "Star Wars" program). This application was communicated to us by scientists from TRW Systems, an SDI contractor, who chose the spacefilling curve heuristic over alternatives because it was well-analyzed, parallelizable, and could run on a computer that was boostable to orbit.
To control a pen-plotter for the drawing of maps. (M. Iri and co-workers at the University of Tokyo showed how it could be used to reduce drawing time for large road maps by routing the pen efficiently. They gave an example in which drawing time was reduced from ten hours to one-half of one hour.)

The idea of routing by spacefilling curve has subsequently been incorporated into the ARC/Info Geographical Information System, the CAPS Logistics Toolkit of Baan Systems, and other commercial systems managing 2-dimensional data.

A summary of the ideas, minus technical details but with pointers to technical literature, may be found in my class notes A routing system based on spacefilling curves [pdf format, 22 pages]. To accompany this is a table of Sierpinski indices of the points of a 100 x 100 grid [pdf format, 22 pages], with which you can set up your own routing system in an afternoon. Technical details about algorithm performance, along with citations to related work, may be found in “Spacefilling curves and the planar travelling salesman problem” with L. K. Platzman, Journal of the Association for Computing Machinery 36(4):719-737 (1989).

Figure 2: A TSP tour of 15,112 cities in Germany. This tour was induced by the Sierpinski spacefilling curve in less than a second and is about 1/3 again as long as the shortest possible.

It is interesting to compare this lightweight heuristic with a heavy-duty optimization package, such as the one developed by D. Applegate, R. Bixby, V. Chvatal, and W. Cook. Their TSP package is a tour-de-force of mathematical optimization technology and it has been used to solve a traveling salesman problem for 15,112 cities in Germany. This is the largest non-trivial problem for which a provably optimal solution has been generated. Applegate et al. describe the computational resources used: “The computation was carried out on a network of 110 processors located at Rice University and at Princeton University. The total computer time used in the computation was 22.6 years, scaled to a Compaq EV6 Alpha processor running at 500 MHz. The optimal tour has length 1,573,084 in the units used in TSPLIB; this translates to a trip of approximately 66,000 kilometers through Germany.”

For comparison, Paul Goldsman used the spacefilling curve heuristic to solve the same instance. Our solution was about 34% longer (Figure 2). At a leisurely 600 km of travel per day this means the total driving time would be about 147 days versus 110 days. But our computation took less than a second on a cheap laptop. So here is the tradeoff: Use our heuristic and you get a route immediately, but you must travel for an extra month. Alternatively, configure a network of 110 processors and spend two months to compute the shortest route — to save a month of driving.

Figure 3: All the points of a triangulated irregular network can be indexed continuously by finding a Hamiltonian path or circuit of the triangles and filling each with a suitably-oriented spacefilling curve.

Bill Nulty, Paul Goldsman, and I have extended some of these ideas in several directions:

"Robust Multidimensional Searching with Spacefilling Curves" by J. Bartholdi and W. Nulty, Proceedings of the Sixth International Symposium on Spatial Data Handling, Edinburgh, Scotland, September 1994.
Continuous indexing of hierarchical subdivisions of the globe by J. Bartholdi and P. Goldsman (2000). This appeared in slightly revised form in Int. J. Geographical Information Science 15(6):489-522 (2001).
Vertex-labelling algorithms for the Hilbert spacefilling curve by J. Bartholdi and P. Goldsman (2000). This appeared in slightly revised form in Software -- Practice and Experience 31:395-408 (2000).
The vertex-adjacency dual of a triangulated irregular network has a Hamiltonian cycle by J. Bartholdi and P. Goldsman, Operations Research Letters 32 (2004). Perouz Taslakian has produced a very nice illustration of the ideas and algorithm.